
Zadanie Biuro podróży (biu)
Pomóż nam usprawnić bazę zadań!
Biuro podróży
Limit pamięci: 128 MB
Bajtazar jest nauczycielem w szkole podstawowej w Bajtołach Dolnych. Korzystając z tego, że pogoda całkiem dopisuje, Bajtazar chciałby zabrać swoją klasę na wycieczkę autokarową do stolicy kraju, Bajtogrodu. Do pomocy w organizacji wycieczki Bajtazar postanowił zatrudnić biuro podróży BajTour.
Ulice w centrum Bajtogrodu tworzą regularną siatkę: każda ulica biegnie albo z zachodu na wschód, albo z południa na północ, a odległości między dwiema sąsiednimi równoległymi ulicami są równe i wynoszą jeden kilometr. Przy niektórych skrzyżowaniach znajdują się atrakcje turystyczne. Bajtoccy przewodnicy każdej atrakcji przypisali pewien współczynnik ciekawości: im wyższy współczynnik, tym dana atrakcja jest ciekawsza dla zwiedzających. Bajtazar wie, że jego podopieczni szybko się nudzą, dlatego chciałby, aby kolejno zwiedzane atrakcje miały coraz większe współczynniki ciekawości.
Biuro BajTour zgodziło się spełnić wymagania Bajtazara, ale przy tym chciałoby na wycieczce jak najwięcej zarobić. Biuro pobiera stałą stawkę jednego bajtalara za każdy kilometr trasy autokaru. Przejeżdżając między dwiema kolejnymi atrakcjami na trasie zwiedzania, autokar porusza się zawsze najkrótszą trasą biegnącą wzdłuż ulic Bajtogrodu. Ponadto, BajTour zarabia w jeszcze inny sposób: zarządcy niektórych atrakcji płacą biuru za przyprowadzanie wycieczek.
Celem BajTouru jest zaproponować trasę zgodną z warunkami postawionymi przez Bajtazara, która zagwarantuje BajTourowi możliwie największy zysk. Czy pomógłbyś w wyznaczeniu odpowiedniej trasy? Uwaga: przejechanie obok atrakcji turystycznej bez wysiadania nie liczy się jako jej zwiedzenie!
Wejście
Pierwszy wiersz wejścia zawiera dwie liczby całkowite  oraz
oraz 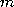 (
(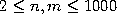 ), oznaczające liczbę ulic biegnących z zachodu
na wschód oraz liczbę ulic biegnących z południa na północ.
), oznaczające liczbę ulic biegnących z zachodu
na wschód oraz liczbę ulic biegnących z południa na północ.
Dalej następuje  wierszy zawierających opis atrakcji turystycznych.
W
wierszy zawierających opis atrakcji turystycznych.
W 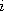 -tym wierszu znajduje się
-tym wierszu znajduje się 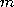 liczb całkowitych
liczb całkowitych 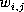 (
(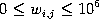 )
oznaczających współczynniki ciekawości atrakcji turystycznych
rozmieszczonych na skrzyżowaniach
)
oznaczających współczynniki ciekawości atrakcji turystycznych
rozmieszczonych na skrzyżowaniach 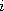 -tej ulicy biegnącej ze wschodu na
zachód z kolejnymi ulicami biegnącymi z południa na północ.
Współczynnik
-tej ulicy biegnącej ze wschodu na
zachód z kolejnymi ulicami biegnącymi z południa na północ.
Współczynnik 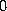 oznacza brak atrakcji turystycznej, natomiast dodatnie
współczynniki opisują poszczególne atrakcje.
Wiadomo, że w Bajtogrodzie jest co najmniej jedna atrakcja turystyczna.
oznacza brak atrakcji turystycznej, natomiast dodatnie
współczynniki opisują poszczególne atrakcje.
Wiadomo, że w Bajtogrodzie jest co najmniej jedna atrakcja turystyczna.
Każdy z kolejnych  wierszy zawiera po
wierszy zawiera po 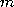 liczb całkowitych
liczb całkowitych 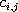 (
(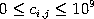 ).
Liczba
).
Liczba 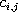 , czyli
, czyli 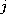 -ta liczba w
-ta liczba w 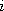 -tym z tych wierszy, oznacza kwotę (w bajtalarach), jaką
biuro otrzymuje za wysłanie wycieczki do atrakcji opisanej współczynnikiem ciekawości
-tym z tych wierszy, oznacza kwotę (w bajtalarach), jaką
biuro otrzymuje za wysłanie wycieczki do atrakcji opisanej współczynnikiem ciekawości 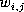 .
Jeśli przy skrzyżowaniu nie ma atrakcji, odpowiadająca mu liczba
.
Jeśli przy skrzyżowaniu nie ma atrakcji, odpowiadająca mu liczba 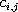 jest równa
jest równa 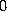 .
.
Wyjście
Pierwszy i jedyny wiersz wyjścia powinien zawierać jedną liczbę całkowitą, oznaczającą (wyrażony w bajtalarach) zysk z najbardziej dochodowej dla biura trasy, odwiedzającej pewne atrakcje turystyczne w kolejności ściśle rosnących współczynników ciekawości.
Przykład
Dla danych wejściowych:
4 5 1 2 6 0 2 1 3 4 0 4 0 0 4 0 3 2 2 0 0 4 1 3 5 0 2 2 8 1 0 2 0 0 3 0 4 0 5 0 0 3
poprawną odpowiedzią jest:
39
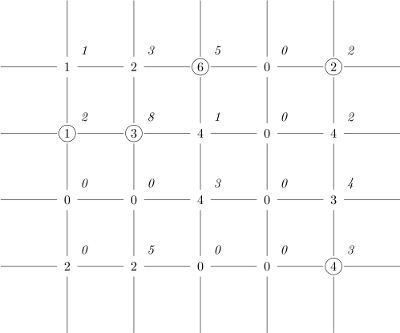
Wyjaśnienie do przykładu:
Liczby napisane na rysunku krojem prostym oznaczają współczynniki ciekawości atrakcji,
a liczby napisane krojem pochyłym - dochody BajTouru za wysłanie wycieczki
do poszczególnych atrakcji.
Atrakcje odwiedzane na najbardziej dochodowej dla biura trasie zwiedzania są zaznaczone kółkami.
Za wysłanie wycieczki do tych atrakcji biuro otrzyma, kolejno, 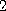 ,
, 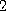 ,
,  ,
, 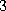 i
i 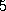 bajtalarów.
Dodatkowo, sumaryczny koszt przejazdu autokaru to
bajtalarów.
Dodatkowo, sumaryczny koszt przejazdu autokaru to 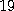 bajtalarów.
bajtalarów.
Autor zadania: Jakub Radoszewski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English